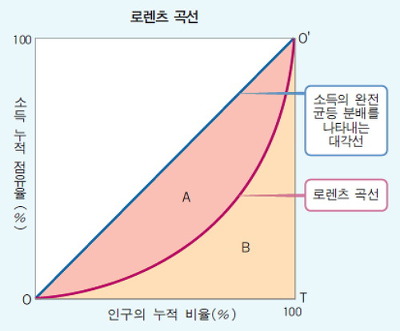
지니계수는 소득 불평등 정도를 나타내는 소득분배 지표입니다.
지니계수는 0~1 사이의 값을 갖고 로렌츠 곡선을 이용해 구할 수 있습니다
소득 분배율이 일정할때 로렌츠 곡선은 y=x 와 일치하게 되고 이때의 직선을 완전평등 대각선이라고 합니다.
$$2\int_0^1 \sin x-L(x)~dx$$
지니계수의 정의는 위와 같습니다. 이를 이용해 프로그램을 작성해보았습니다.
$L(x)$는 로렌츠 함수입니다.
from sympy import Integral, Symbol
x = Symbol('x') #x의 문자 변수화
Lx = 0.7 * x**2 + 0.3 * x
f = x
result = Integral(f = Lx, (x,0,1)).doit() #0부터 1까지 정적분
print('지니 계수 : ', 2 * result)
result = round(2 * result , 2)
print('반올림 값 : ', result)
if result == 0:
print('완전 평등')
elif 0 < result <= 0.2:
print('매우 평등한 사회')
elif 0.2 <= result < 0.4:
print('비교적 평등한 사회')
elif 0.4 <= result < 0.6:
print('불평등한 사회')
else:
print('매우 불평등한 사회')
위 예제는 $L(x) = 0.7x^2 + 0.3x$ 일 때의 지니계수를 구하는 예제입니다.

더 참고할만한 것 - http://www.index.go.kr/potal/main/EachDtlPageDetail.do?idx_cd=1407
'프로그래밍 > Python' 카테고리의 다른 글
| [Python] Selenium + 끄투핵 (0) | 2019.12.05 |
|---|---|
| [Python] Requests 와 Fiddler 동시에 이용하기 (0) | 2019.12.01 |
| [Python] 리로스쿨 로그인 + 내신 가져오기 (0) | 2019.11.29 |
| [Python] 로또 회차별 당첨번호 분석 (0) | 2019.11.17 |
| [Python] 파이썬으로 미분하기 (평균변화율 , 미분계수) (0) | 2019.11.04 |









