pip install sympy파이썬으로 미분을 위해선 sympy 모듈 설치가 필요합니다.
평균변화율

평균변화율 공식을 이용하여 함수의 평균변화율을 구할 수 있습니다.
두 점의 평균 변화율은 두 점을 지나는 직선의 기울기와 같습니다.
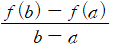
b 점과 a 점의 평균변화율은 다음과 같은 식으로 구할 수 있습니다.
다음은 함수 x^2 + 2x + 4 위의 점 (0 , 4) 와 (2, 12) 의 평균 변화율을 구하는 함수입니다.
from sympy import symbols
def average(a,b):
m = max(a,b)
n = min(a,b)
x = symbols('x') #기호변수 선언
fx = x ** 2 + 2 * x + 4 # x^2 + 2x + 4 라는 함수 정의
fb = fx.subs(x, m) #함수에 m대입
fa = fx.subs(x, n) #함수에 n대입
result = (fb - fa) / (b - a)
return result
print(average(0,2))
>>> 4sympy의 symbols 를 이용해 x를 기호변수로 바꾸고
fx 를 정의한후 fx.subs(변수, 대입값) 을 이용하여 y값을 구합니다.
그후 공식을 이용해 평균변화율을 구합니다.
미분계수

함수 f(x)의 한점 a 점에서의 순간변화율을 구하면 그것이 즉 a점에서의 접선의 기울기가 됩니다.
f(x)를 미분하여 얻은 함수를 도함수라고 하고 이 함수는 f(x) 그래프 기울기의 순간적인 변화율을 나타냅니다.
(위 수식에서 델타 x를 변수 x로 변경하고 lim x -> 0으로 보낸 식입니다.)
도함수를 구한후 a를 대입하게 되면 a점에서의 순간변화율을 구할 수 있습니다.
from sympy import Derivative, symbols
x = symbols('x') #x를 기호변수화
fx = 4 * x ** 4 + 3 * x ** 3 + 2 * x ** 2 + x + 1
fprime = Derivative(fx, x).doit() #x에 대해서 미분
print("fx 의 도함수는 : ", fprime, "입니다")
n = fprime.subs({x: 3})
print("fx에서 x = 3 에서의 순간변화율(미분계수는) ", n , "입니다")
>>> fx 의 도함수는 : 16*x**3 + 9*x**2 + 4*x + 1 입니다
>>> fx에서 x = 3 에서의 순간변화율(미분계수는) 526 입니다Derivative 함수를 이용하여 정의한 fx 를 간편하게 도함수로 바꿀 수 있습니다.
기호로 나타내다보니 함수가 보기 좀 힘들지만.. 이해가 바로 안되시면 종이에 한번써보는걸로 ㅎㅎ...
from sympy import Derivative, symbols
x = symbols('x') #x를 기호변수화
fx = 4 * x ** 4 + 3 * x ** 3 + 2 * x ** 2 + x + 1
fprime = Derivative(fx, x) #x에 대해서 미분
print("fx 의 도함수는 : ", fprime, "입니다")
n = fprime.doit().subs({x: 3})
print("fx에서 x = 3 에서의 순간변화율(미분계수는) ", n , "입니다")
>>> fx 의 도함수는 : Derivative(4*x**4 + 3*x**3 + 2*x**2 + x + 1, x) 입니다
>>> fx에서 x = 3 에서의 순간변화율(미분계수는) 526 입니다끝에 .doit()을 붙여주지 않으면 객체만 생성되고 도함수로 바뀌지 않음을 출력값을 확인해 알 수 있습니다.
값을 구할때 끝에 doit 을 붙여주고 subs를 이용해 값 대입을 처리하면 똑같이 구할 수 있음을 알 수 있습니다.
어떻게하든 끝에 doit 을 넣어주시면 됩니다.
이계 도함수
from sympy import Derivative, symbols
x = symbols('x') #x를 기호변수화
fx = 4 * x ** 4 + 3 * x ** 3 + 2 * x ** 2 + x + 1
fprime = Derivative(fx, x).doit() #x에 대해서 미분
print("fx 의 도함수는 : ", fprime, "입니다")
fdoubleprime = Derivative(fprime, x).doit() # fprime 에 대하여 미분
print("fx의 이계도함수는 : ", fdoubleprime, "입니다")
>>> fx 의 도함수는 : 16*x**3 + 9*x**2 + 4*x + 1 입니다
>>> fx의 이계도함수는 : 48*x**2 + 18*x + 4 입니다이계 도함수는 도함수의 값을 한번더 미분한 함수입니다. 이차 도함수라고도 합니다.
정의에 의해 그냥 한번더 Derivative 를 이용해 미분해주면 구할 수 있습니다
'프로그래밍 > Python' 카테고리의 다른 글
| [Python] Selenium + 끄투핵 (0) | 2019.12.05 |
|---|---|
| [Python] Requests 와 Fiddler 동시에 이용하기 (0) | 2019.12.01 |
| [Python] 리로스쿨 로그인 + 내신 가져오기 (0) | 2019.11.29 |
| [Python] 정적분과 지니 계수 구하기 (0) | 2019.11.17 |
| [Python] 로또 회차별 당첨번호 분석 (0) | 2019.11.17 |









