* 본 글은 학부생의 눈높이에서 작성되었습니다. 잘못된 부분이 있을 수 있으며 발견시 댓글로 정정부탁드립니다.
또한 이유없는 비방은 삭제처리될 수 있으니 유의 바랍니다.
What is K-maps?

오늘 알아볼 것은 카르노 맵입니다. 카르노 맵이란 한마디로 복잡한 부울식을 복잡한 식 계산 없이 그림으로 그려 쉽게 간소화 시켜주는 도구입니다. 여기서 간소화는 복잡한 식을 동일한 더 적은 글자수와 더 적은 항들로 나타낼 수 있다는 의미가 됩니다.
디지털 회로 설계를 할때 AND Gate, OR Gate 등 여러 Gate를 사용하게 되는데 이를 표현할때 위 사진과 같은 부울식을 사용하게 됩니다. 부울식을 통해 회로를 설계할것이기 때문에 부울식을 간소화하게 되면 동일한 기능을 하면서 더 적은 Gate, 간략화된 회로를 구성할 수 있게 되므로 이러한 부울식의 간소화(=최적화)는 중요한 과정입니다.
설명에 앞서서 AND 연산의 경우 $A·B$ 와 같이 가운뎃점을 이용해 나타낼 것인데 이건 생략이 가능하므로 생략하도록 하고 OR연산의 경우 $A+B$, +기호로 나타내도록 하겠습니다. (우리가 알던 산술연산, 즉 덧셈이 아니니 주의하셔야 합니다. )
또한 $F$의 Compliment(not) 는 F바 즉, $\bar{F}$ 로 나타내도록 하겠습니다.
Minterm and Maxterm
카르노 맵의 사용방법에 앞서 Minterm과 Maxterm에 대해 알아보겠습니다. (이에 대해 이미 알고 계시면 스크롤을 쭉 내려서 카르노 맵에 대해서만 읽어보셔도 됩니다.) 카르노맵을 사용하게 될 수 밖에 없는 상황이 오는데 바로 Minterm 과 Maxterm 이라는 것 때문입니다.
만약 예를 들어서 $A,B,C$ 라는 변수가 있는데, 부울식을 작성할때 전부 AND연산으로 계산해주면 $ABC$가 되겠죠. 근데 이걸 누군 $BAC$라고 쓰고 누구는 $BCA$ 라고 쓰면 매우 혼란스럽겠죠?
그래서 부울식을 작성할때 Canonical Form(정형화된 양식) 의 필요성이 대두되게 됩니다.
이렇게 Canonical Form을 작성하기 위해 있는 녀석들이 바로 Minterm 과 Maxterm 입니다.
Minterm
우선 Minterm에 대해 알아봅시다. Maxterm보다도 훨씬 많이 쓰이는게 Minterm인데 카르노맵도 사실 Minterm 식을 최적화 하기 위한 도구입니다.
Minterm의 형식으로 나타내기 위해선 모든 변수를 작성해줘야 하고 알파벳 순서로 나타내야 합니다.
또 모든 변수는 AND연산으로 묶여야 합니다.
위 셋 중 하나라도 안지키면 Minterm 형식이 아닙니다.
예를 들어서 변수 $A,B,C,D$ 가 있다고 치면
만약 $ABCD$ 의 경우 알파벳 순서로 지켜졌고, 모든 변수가 AND 연산으로 묶여 있고 모든 변수 $A,B,C,D$ 가 적혀있으니 Minterm의 형태가 맞습니다.
$ABC$ : 알파벳 순서가 지켜졌지만 모든 변수가 작성되지 않았으므로 Minterm 형태가 아닙니다.
$BACD$ : 알파벳 순서가 아니므로 안됩니다.
$ABC+D$ Minterm의 모든 변수는 AND 연산으로 묶여야 합니다. OR연산이 포함되서 안됩니다.
Maxterm
Maxterm의 경우 Minterm과 특징이 반대인 형태라고 보시면 됩니다.
우선 Maxterm의 형식으로 나타내기 위해선 모든 변수를 작성해줘야 하고 알파벳 순서로 나타내야 합니다. (여기까진 Minterm의 규칙과 동일하죠)
그러나 모든 변수가 OR 연산으로 묶여야 합니다.
위 셋 중 하나라도 안지켜지면 Maxterm 형태가 아닙니다.
예를 들어서 변수 $A,B,C,D$ 가 있다고 치면
$A+B+C+D$ : 모든 변수가 OR 연산으로 묶였고, 알파벳 순서로써 모든 변수가 표현되었으므로 Maxterm 형태가 맞습니다
$A+B+C$ : 모든 변수가 작성되지 않아서 Maxterm 형태가 아닙니다.
$AB+CD$ : 모든 변수가 OR연산으로 묶여야 합니다. AND 연산이 섞여 있으므로 안됩니다.
$B+A+C+D$ : 알파벳 순서가 아니므로 안됩니다.
SOM(Sum of Minterm) 과 POM (Product of Maxterm)
부울식을 쓸때 Canonical Form으로써 Minterm과 Maxterm을 사용한다는거 까진 이해하셨을 겁니다.
그런데 이 Minterm 과 Maxterm을 과연 어떻게 활용할지 의문이 생기죠.
사실 Minterm 과 Maxterm 은 굉장히 유용한 도구로써 사용될 수 있는데
바로 진리표를 부울식으로 바꿔낼때 사용하게 됩니다.
우선 시작전에 아래 규칙을 숙지합니다.
Minterm의 경우
0 -> $\bar{X}$ 로 매칭
1 -> $X$ 로 매칭
정의상 함수의 OUTPUT에서 1만 뽑아서 나열한 것
Maxterm의 경우
0 -> $X$ 로 매칭
1 -> $\bar{X}$ 로 매칭
정의상 함수의 OUTPUT에서 0만 뽑아서 나열한 것
아직 까지는 무슨 소리인지 잘 모르시겠죠? 아래 진리표를 봐봅시다.
| A | B | O |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
다음은 INPUT A,B 와 출력 O 의 진리표 입니다.
O를 출력 함수라고 생각하시고 A,B로 나타낸다고 하면 어떻게 해야하나요?
이 진리표는 익숙하시죠. A와 B의 OR 연산의 결과값 입니다.
부울식으로 나타내면
$O = A + B$ 로 나타내어짐이 자명하죠?
그런데 만약에 이렇게 작은 진리표 말고 매~우 크고 복잡한 진리표로 바뀐다면
O라는 함수를 쉽게 다른 INPUT 변수들의 부울식으로 바꿔내기가 어렵겠죠?
우선은 위 진리표를 Minterm 표현에 따라 부울식으로 바꿔보고 더 큰 진리표도 부울식으로 바꾸는걸 보여드리겠습니다.
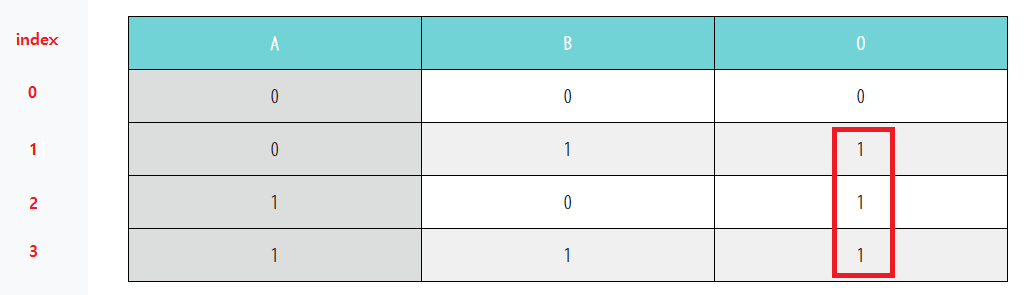
아까도 말했듯이 Minterm 의 경우 정의상 함수의 OUTPUT에서 1만 뽑아내서 나열한 걸 말합니다.
빨간색 부분이 Output 에서 1만을 선택한 것이구요.
보시면 왼쪽에 index라는 것이 추가 됬는데 말그대로 위 0부터 차례대로 순번을 매겨둔 것이라고 보시면 됩니다.
우리는 output에서 1을 뽑아둔 것과 저 인덱스를 활용하여 진리표를 부울식으로 바꿔낼 것입니다.
우선 1이 뽑힌 부분은 인덱스(순번) 상 1, 2, 3번 입니다.
INPUT 값이 2개의 비트이므로 ($A,B$) 1, 2, 3 을 2개의 비트로써 2진수로 바꿔내면
01, 10, 11 이 되게 됩니다.
그러면 Minterm의 매칭 규칙인
0 -> $\bar{X}$ 로 매칭
1 -> $X$ 로 매칭
에 따라서 각 변수로서 바꿔낼 수 있습니다.
01의 경우 첫번째 비트를 A, 두번째 비트를 B라고 한다면
01 -> $\bar{A}B$ 로 나타내집니다. (Minterm의 형태로써)
나머지 방법도 같은 방법으로 진행하면
10 -> $A\bar{B}$
11 -> $AB$
로 나타내집니다.
이제 01, 10, 11은 각각 $\bar{A}B$, $A\bar{B}$, $AB$ 로 나타내지는걸 알았으니깐
이걸 OR연산 $+$ 으로 전부 묶습니다.
$\bar{A}B$ + $A\bar{B}$ + $AB$ 라는 식이 완성되었습니다.
이것이 바로 OUTPUT 값 O의 식
O = $\bar{A}B$ + $A\bar{B}$ + $AB$ 이 되게 됩니다.
실제로 값을 넣어보면 위 진리표에 맞게 부울식이 만들어진 것을 알 수 있습니다.
각 항은 Minterm 형태로 표현되었고 각 항들이 전부 OR 연산에 의해 묶였는데 OR 연산의 기호인 $+$ 가 마치 더하는 기호 같다고 해서 $\bar{A}B$ + $A\bar{B}$ + $AB$ 와 같은 표현을 Sum of Minterm (Minterm의 합) 이라고 하고 줄여서 SOM 이라고 합니다.
SOM 표현으로 나타내라는 뜻이 나오면 앞으로는 각 항은 Minterm으로, 나머지는 전부 OR 연산으로 묶여있는 형태로 나타내라는 뜻으로 이해하면 됩니다.
그런데 뭔가 마음에 들지 않지 않나요?
출력 함수의 식이 O = $\bar{A}B$ + $A\bar{B}$ + $AB$ 를 구하긴 했습니다만
처음에 O라는 함수의 식은 우리가 처음 봤듯이 O = $A+B$ 라고 알고 있잖아요?
실제로 위 두식은 똑같은 회로지만, Minterm으로 뽑힌 식이 최적화가 되어있지 않은 겁니다.
부울식의 여러 성질(Boolean Identities)들을 이용해서 식을 간략화를 해보면 아래와 같습니다.


보시면 결론적으로 식이 똑같습니다. 이렇게 같은 부울식으로써 항들과 변수를 줄이는 과정을 간략화(최적화) 라고 하는데 이렇게 수학적 식으로 간략화를 할 수 있습니다.
Minterm은 어떤 회로던 간에 진리표만 있으면 부울 식으로 바꿔내서 회로를 구성할 수 있는 아주 강력한 도구(?) 이지만 모든 항을 나열하는 방식으로 식을 구성하기 때문에 이렇게 최적화를 하는 과정이 꼭 필요합니다.
그런데 위 정도 식이면 그렇게 식이 길다곤 할 수 없습니다 Minterm으로 식을 뽑았는데 만약에 엄청나게 긴 식이 있다면 저렇게 수학적으로 적으면 최적화 과정이 복잡하고 엄청 길어지겠죠?
이 최적화 과정을 수학적인 식을 써서 하는 방법이 아닌, 시각적인 방법으로써 (그림을 그려서) 최적화 하는 도구가 바로 오늘 알아볼 카르노 맵(K-MAPS) 입니다.
카르노 맵에 대한 이야기는 아래에서 하고 우선 Maxterm에 대해서도 알아봅시다.

Maxterm 의 경우 정의상 함수의 OUTPUT에서 0만 뽑아내서 나열한 걸 말합니다.
빨간색 부분은 아까 Minterm 을 선택했던 부분이니 무시해주시고
0만을 선택하는건 인덱스 0번 밖에 없네요.
변수가 A, B 두개이므로 0을 비트 2개로써 나타내면 00이고
Maxterm의 규칙
0 -> $X$ 로 매칭
1 -> $\bar{X}$ 로 매칭
를 통해 매칭시키고 Maxterm으로써 표현하면
A+B가 되겠네요.
아까와 똑같이 출력함수 O에 대해서 식이 잘 뽑혔죠?
1만을 나열해서 Minterm을 뽑아서 식을 구성하나, 0만을 나열해서 Maxterm을 뽑아서 식을 구성하나 결론적으로는 같은 식이 나옵니다.
그러므로 진리표를 Minterm이나 Maxterm으로 뽑을때는 0과 1의 갯수를 보고 더 빨리 식이 나올만한걸 고르는게 일단은 효율적이겠죠.
그리고 지금의 경우 0이 하나밖에 없어서 A+B라는 식으로 결과가 끝나지만
0이 더 있었다면 Maxterm의 형태로 표현된 여러 식이 있었을 겁니다.
항이 여러개라면 Maxterm의 항들의 값들은 AND연산으로 묶게 되는데
AND연산의 기호 $·$ 점을 product라고 하므로 이러한 식들은 Maxterm의 Product(곱) 인 POM 이라고 합니다.
*제가 예시로 너무 단순한 걸 가져와서 POM식을 못 보여드리는게 좀 아쉽네요 ㅎㅎ;;

추가적으로 O라는 함수는 minterm 표현으로 인덱스의 1,2,3을 전부 택한 형태입니다.
수학적으로는 소문자 m을 사용해서 $O = m_{1} + m_{2} + m_{3}$ 으로 나타내고
조금더 간략화된 표현으로는 $\sum_{m}(1,2,3)$ 으로 나타냅니다.
또 O라는 함수는 maxterm 표현으로 인덱스의 0을 택한 형태입니다. (0이 더 있었다면 0을 전부 택했을 겁니다.)
수학적으로는 대문자 M을 이용해서 $O = M_{0}$으로 나타내고
조금더 간략화된 표현으로는 $\prod_{M}(0)$ 로 나타낼 수 있습니다.
정리하여 $O =$ $\sum_{m}(1,2,3)$ = $\prod_{M}(0)$ 입니다.
그리고 또한 Minterm과 Maxterm은 Compliment 관계 입니다. Minterm 식에 Not 연산을 취해주면 그것은 바로 Maxterm 식이 됩니다.
쉽게 이야기 해서 Minterm이 아니면 Maxterm이라는 뜻입니다. (Maxterm아니면 Minterm)
인덱스가 4번까지 있으면 Maxterm에 해당하는 인덱스가 0번이면 Minterm의 경우는 Maxterm 을 제외한 그 이외 모든 것 즉 인덱스 1,2,3 번 입니다. (그 예시가 바로 위 O의 식이 되겠죠.)
* 이러한 특성을 이용해서 카르노맵 최적화를 조금더 빠르게 (똑똑하게) 할 수도 있습니다.
카르노맵
카르노맵은 아까도 말했듯이 일반적으로 진리표를 Minterm을 이용해서 부울식으로 바꿨을때 그 식을 간소화 하기 위한 도구입니다. (Maxterm도 있으나 일반적으로 Minterm 이 많이 사용되므로, 카르노맵은 Minterm을 간략화 하기 위해 사용합니다.)
변수가 2개인 식의 경우 너무나도 간단해서 일반적으로 최적화 할 필요가 없거나 Boolean Identities 를 이용해서 쉽게 간소화가 되기 때문에 변수가 3개인 식부터 다루겠습니다.
3변수 카르노맵

우선 변수가 $X, Y, Z$ 처럼 3개로 이루어진 식을 최적화 할때는 3변수 카르노맵을 사용합니다.
카르노맵은 그림을 그려서 최적화를 하는데, 표를 그릴때 변수가 바뀌는 모든 경우의 수를 적어주면 됩니다.
위 표의 경우 왼편에는 X라는 변수는 0또는 1을 가질 수 있으므로 0 , 1이라고 적어주었고
위 표의 경우에는 Y, Z라는 변수가 각각 0또는 1을 가지는 모든 경우의 수를 나열해서 적어주었습니다. (각 비트가 2개의 경우의 수를 가지므로 총 경우의 수는 $2^2$개로 계산됩니다.)
그리고 순서가 XYZ순이므로 X, Y, Z의 이진수 값을 읽어낸 것이 아까 말했던 minterm의 index 번호에 대응되게 됩니다.
예를 들어서 X=0, Y=1, Z= 1 인 경우 XYZ 순서이므로 011 은 10진수로 3이므로 minterm의 3번째 인덱스 항 $m_{3}$ 이 되게 되는 것입니다.
*위 그림에서 YZ = 11 은 Y=1, Z=1과 동일 표현입니다.

카르노 맵을 그릴때 가장 중요한 점은 순서가 0,1,2,3이 아니라 0,1,3,2 입니다. 반드시 인접한 비트가 1비트씩 바뀌도록 해야 합니다. (01 -> 10 으로 비트가 2개씩 바뀌면 안된다는 겁니다.) 인접이라고 하면 바로 옆칸에 이웃한 것들을 이야기 합니다. 이렇게 하는 이유는 부울식을 이용해 최적화를 할때 한 비트씩 바뀌는 것들을 묶어서 최적화 하는 경우를 고려해서 이렇게 만든 것 입니다.
우선 일반적으로 순서 자체를 쓸때 뒤 2칸의 순서가 역전된다 라는걸 기억하고 인덱스 순서 자체를 외워서 사용해주시면 됩니다.

그리고 카르노 맵을 그리고 변수를 표시하는 방법은 매우 여러가지가 있는데 제가 봤을때 가장 간편한 방법은 각 변수가 1이 되는 부분에 X, Y, Z로 표시를 해두는 것 입니다. 이렇게 하면 최적화 이후 변수를 읽어낼때 매우 간편해지게 됩니다.
(좀 있다가 왜 이렇게 하는지 이해하시게 될 것 입니다.)
왼쪽 사진에 보면 각 변수 X ,Y, Z 가 1이 되는 부분에 칸막이를 쳐서 구분을 해뒀습니다. 그리고 나머지 0인 부분은 Compliment 표시를 해뒀는데 어짜피 X아니면 X바이기 때문에 (1 아니면 0이기 때문에) 바 부분은 따로 표시하지 않을 것 입니다.
$F(X,Y,Z)=\sum_{m}(2,3,6,7)$
이제 한번 다음식의 최적화를 진행해 보겠습니다.
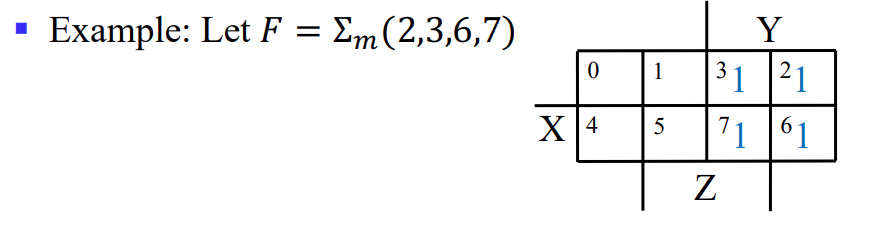
우선 아까와 똑같이 3변수 카르노맵을 그립니다. X,Y,Z 의 모든 비트 경우의 수를 나열한 다음에 1이 되는 부분만 X,Y,Z 로 표시해주고 나머지는 다 지워버립니다.
그리고 각 인덱스에 해당하는 부분에 1로 표시를 해줍니다.
우리의 목표는 저 1이라는 부분을 네모로 묶어서 전부 커버하고, 그 네모를 식으로 읽어내면 최적화된 minterm 식을 얻을 수 있습니다.
* 1로 표시되지 않는 부분의 경우엔 전부 0으로 채워져 있다고 생각합니다. 1만을 묶을 것이라 0은 안쓰고 생략해도 됩니다.
카르노맵에서 1을 네모로 묶을때 아래 규칙을 반드시 전부 지켜야 합니다!!
아래 규칙을 잘 모르고 진행하면 반드시 햇갈리고 틀리게 될 가능성이 큽니다.
1. 네모는 $2^n$ 의 크기로 묶어야 한다. (1, 2,4,8,...)
=> 예를 들어서 6개씩은 묶을 수 없습니다.
1개씩 묶는것도 가능하니 알아둡시다. 가끔 시험장에서 minterm 표시를 했는데 1이 다 떨어져 있어서 안묶여서 당황하는 경우가 생깁니다...
2. 네모는 최대한 크게 묶는다.
=> 카르노 맵에서 네모의 크기가 클수록 변수의 갯수가 줄어들게 됩니다. 최적화의 목적은 변수를 최대한 줄이고 항을 줄이는 것이기 때문에 네모의 크기를 최대한 크게 묶어야 합니다.
3. 네모의 갯수는 최소가 되도록 묶는다.
=> 카르노 맵에서 네모의 갯수는 곧 항의 갯수입니다. 최적화의 목적은 변수를 최대한 줄이고 항을 줄이는 것이기 때문에 네모의 갯수는 최소가 되도록 묶어야 합니다.
4. 카르노 맵의 위 아래와 양 옆은 연결되어 있다.
=> 카르노 맵에서 인접해있을때 비트가 한비트씩 바뀌도록 하였습니다. 위 아래 양 옆의 경우에도 비트가 하나씩 바뀌는 부분이 있기에 연결되어 있는 것 입니다.
그래서 위 아래와 양 옆이 떨어져 있는 것 처럼 보여도 실제로 네모로 묶어낼 수 있습니다.
5. 1을 전부 묶어야 한다.
=> 네모를 다 묶었는데 1이 남아버리면 안됩니다.
6. 무관항(Don't Care) 의 경우 식을 최적화 하는데 도움이 되면 묶고, 만약에 그렇지 않으면 묶지 않아도 된다.
=> Don't care의 경우에는 0이 되던 1이 되던 상관이 없기 때문에 최적화에 도움이 되면 1로 취급해서 묶고, 도움이 안되면 0으로 취급해서 묶지 않아도 됩니다.
=> 여기서 최적화에 도움이 된다는 의미는 네모를 더 크게 묶을 수 있게 하거나, 네모의 갯수를 줄이는데 도움을 주는걸 말합니다.
위 법칙을 반드시 명심하고 진행해 봅시다. 위 법칙중에 하나를 위배하면 틀린 답을 얻을 가능성이 매우 매우 높습니다. 전부 지켜야 합니다.
인터넷 글에서 카르노맵 글을 많이 봤는데 이러한 법칙을 미리 명시하지 않아서 햇갈리는 경우가 꽤 많았습니다.
저 네모를 묶을때 PI(Prime Implicant) 를 전부 찾은다음에 EPI(Essential Prime Implicant)를 이용해서 모든 경우의 수를 체계적으로 찾는 방법도 있습니다만 개인적으론 더 햇갈리고 귀찮은 방법이라고 느꼈습니다.
결론적으로 위의 6가지 법칙만 위배하지 않으면 최적해를 얻어낼 수 있습니다.

사실 이 예제의 경우에는 너무 간단하죠. 네모를 최대한 크게, 갯수는 적게 묶어야 하므로 이렇게 묶어낼 수 있습니다.
이제 저 네모 부분을 식으로 읽어내면 $F(X,Y,Z)=\sum_{m}(2,3,6,7)$ 이 식의 최적화된 형태를 얻을 수 있습니다.
각 변수 하나하나씩 보면서 읽어보시면 됩니다.
우선 X의 경우 X하나로 저 1을 전부 포함시킬 수 없습니다. X와 X바 이렇게 2개가 겹쳐버리므로 무시합니다.
Y의 경우에는 Y 부분이 저 1 부분을 전부 포함시킬 수 있습니다. 우선 저 부분은 Y입니다.
Z의 경우에도 Z부분 하나로는 저 1이 전부 포함되지 않습니다. 무시합니다.
그래서 결론적으로는 위 식을 최적화 한 것은 Y 입니다.
$F(X,Y,Z)=\sum_{m}(2,3,6,7) = Y$

만약에 수학적으로 최적화를 진행했다면 이렇게 복잡한 식들을 전개해서 풀어나가야 했을 겁니다.
결과는 같지만 카르노맵이 최적화에 있어서 훨씬 간편한 것을 알 수 있습니다.

또한 카르노 맵의 경우 위아래가 연결되어 있다고 했으므로 이렇게 4개짜리 네모를 만들 수도 있습니다.
물론 결과 값은 같습니다. 지금은 3변수라 비교적 네모를 묶는 방법이 그렇게 많지 않지만, 만약 변수가 늘어나면 네모를 묶는 방법이 더 다양해질 수 있어서
최적화를 했을때 답이 1개가 아니라 더 많이 나올 수 있습니다.
4변수 카르노맵

4변수 카르노 맵의 경우 위와 같습니다. 역시 비트가 바뀌는 모든 경우의 수를 나열해주는데 비트가 1비트씩 바뀌도록 적어주시면 됩니다.
이제 저기서 A, B, C, D가 각 1인 부분만을 표시해주면 아래와 같이 됩니다.
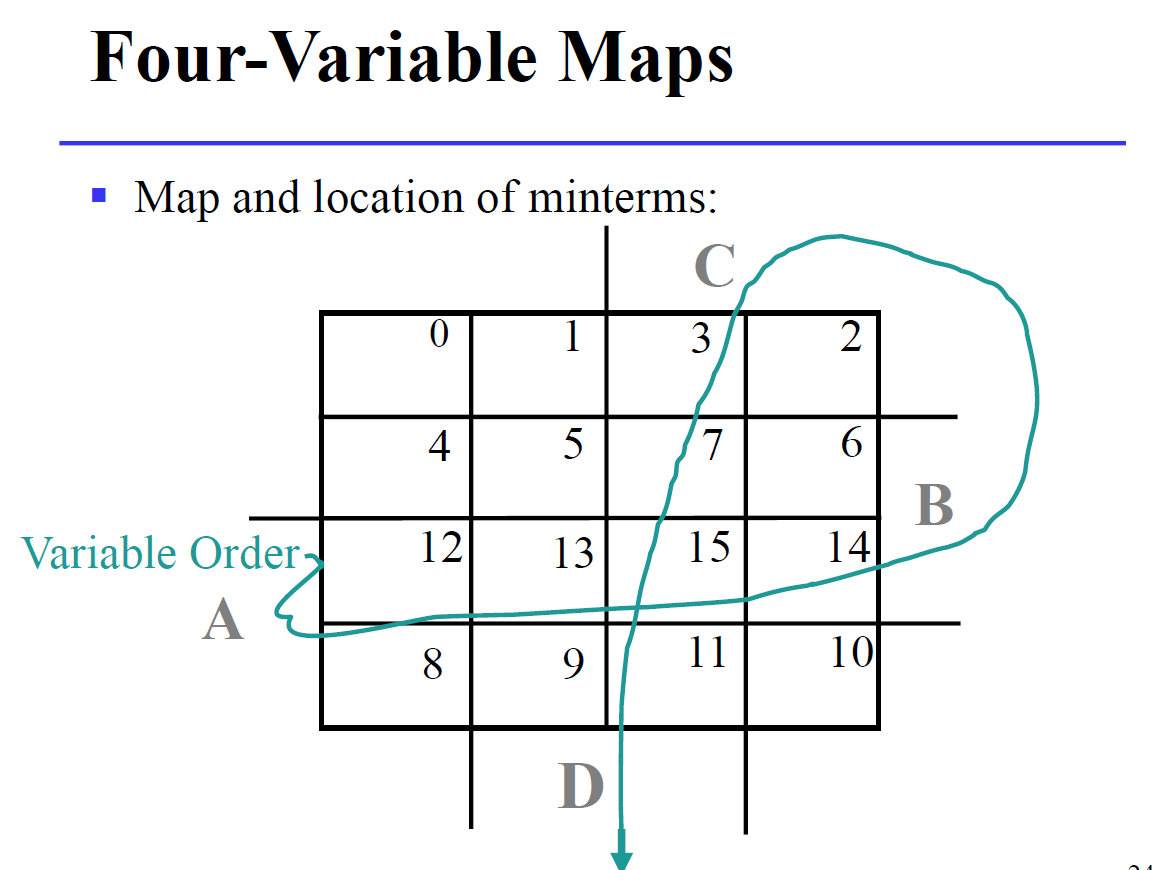
이번에도 순서에 주의하셔야 하는데 8이 되는 부분이 맨 왼쪽 아래에 있습니다.

이유는 이 부분이 이진수로 1000, 8이기 때문입니다. 이것 역시 순서 자체를 통째로 외워주시면 편합니다.
$F(A,B,C,D)=\sum_{m}(3, 4, 5, 7, 9, 13, 14, 15)$
다음 식을 한번 최적화 해보겠습니다.
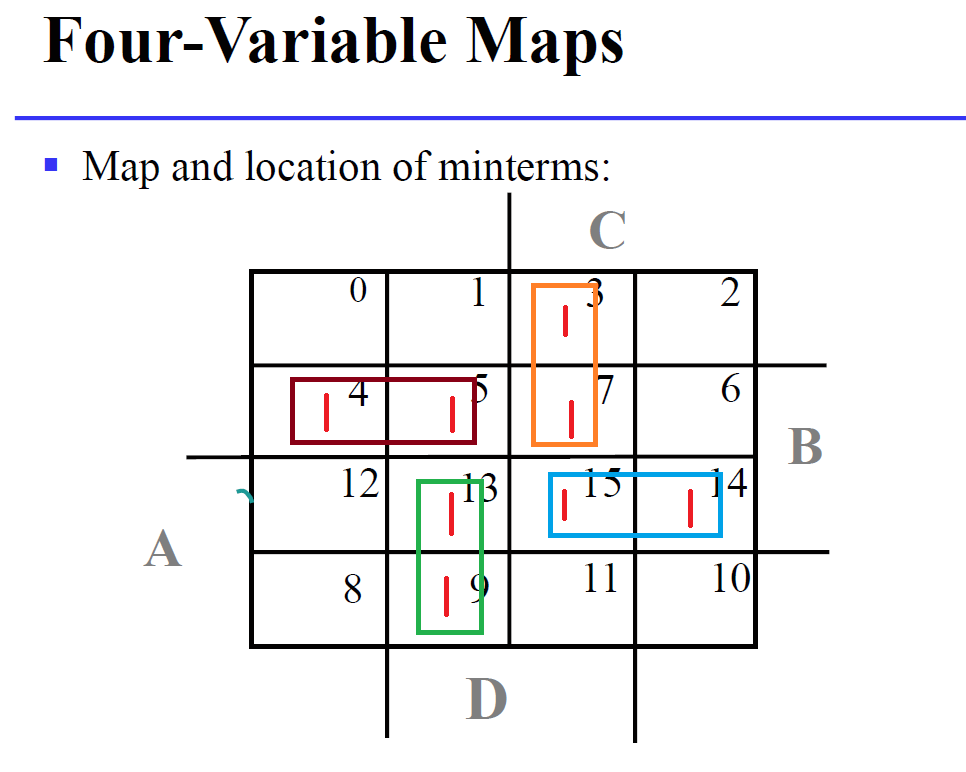
위 아래로 연결을 시켜봐도 큰 사각형을 만들 수 없어서 위 식의 경우 1을 전부 커버시켜 이렇게 그리는게 최적입니다.
즉 $F(A,B,C,D)=\sum_{m}(3, 4, 5, 7, 9, 13, 14, 15) = \bar{A}CD + \bar{A}B\bar{C} + A\bar{C}D + ABC$
가 됩니다.

저는 처음에 이렇게 묶었는데 이렇게 묶으면 틀립니다. 중간에 파란색 네모때문에 항이 더 나오거든요.
1을 전부 커버하면서, 네모의 크기는 최대한 크게, 네모의 갯수는 최대한 작게. 명심합니다.
5변수 카르노맵

W,X,Y,Z,V 와 같이 변수가 5개인 카르노 맵의 경우에는 V가 0, 1이 되는 경우의 수를 나눠서
4변수 카르노맵 2장을 그려서 최적화 합니다.
그런데 5변수 카르노 맵은 앞의 4변수, 3변수에 비해 복잡하기도 하고 잘 쓰이지 않기 때문에 이해만 하고 넘어가도록 하겠습니다.
온라인 카르노맵 계산기
카르노맵으로 최적화 문제를 풀다보면 내가 제대로 네모를 묶어냈는지 햇갈릴때가 있습니다.
그리고 문제를 푸는게 아니라면 이렇게 일일히 그림을 그리는게 귀찮기도 하고, 실수할 가능성도 많겠죠.
그럴땐 아래와 같이 온라인 카르노맵 계산기 사이트를 이용하시면 됩니다.
https://www.charlie-coleman.com/experiments/kmap/
Karnaugh Map Solver
Sum of Products Product of Sums (very slow with >10 variables) Draw Kmap Draw groupings
www.charlie-coleman.com

필요한 변수와 Minterm Index, Don't care (있는 경우) 를 콤마로 구분해서 입력해주면
어떻게 묶는게 최적인지와 그 네모에 맞는 식을 읽어서 최적화를 해줍니다.
간편하죠??
이건 아까 제가 묶어냈던 나선형(?) 문제인데 계산한 값과 똑같이 나왔네요.
무관항에 대한 카르노맵 최적화는 우선 아까 카르노맵 법칙의 6번을 명심하시고 풀면 되므로 본 글에선 생략하도록 하겠습니다. (혹시 댓글로 필요하신 분들이 있으면 본문 내용을 추가하도록 하겠습니다)
많은 도움이 되셨길 바랍니다~
'CS > Digital Logic' 카테고리의 다른 글
| [디지털 논리] 마인크래프트에서 구현한 7 segment 출력 회로 (0) | 2022.05.09 |
|---|







