https://www.acmicpc.net/problem/1463
1463번: 1로 만들기
첫째 줄에 1보다 크거나 같고, 106보다 작거나 같은 정수 N이 주어진다.
www.acmicpc.net
문제 설명
예전에 풀었던 백준 문제 "1로 만들기" 입니다. SolvedAC 기준 실버 3에 위치해 있는 문제로 나름 유명한(?) DP 문제입니다. DP 문제에 잼병인 본인에게는 처음에 DP를 사용해서 풀어야 한다는 걸 듣고 나서도 혼자 해결하진 못했고 아래 유투브 영상을 보고 이해할 수 있었습니다.
일단은 해법을 글로 자세히 설명할 것이긴 한데 유투브 영상을 먼저 올려 놓으면 제 글은 안보고 영상만 보고 나갈꺼 같아서 일단은 영상은 글 맨 말미에 두겠습니다 ㅎㅎㅎ
문제에 대해 간단히 설명을 하자면
임의의 정수 X에 사용할 수 있는 연산이 주어집니다.
1. X가 3으로 나누어 떨어지면 3으로 나눈다
2. X가 2로 나누어 떨어지면 2로 나눈다
3. 1을 뺀다
우리가 임의의 정수 X에 값을 입력하면 저 위의 3가지 연산을 "최소" 로 활용해서 1로 만들 수 있는 연산의 갯수를 찾는것 입니다. 여기서 중요한 건 최소 연산의 갯수를 찾는 다는 것 입니다.
예를 들어서
10이라는 수가 입력되면 위 연산을 최소로 사용해서 1로 만들려면
10 -> 9 -> 3 -> 1 이 됩니다.
1. 1을 뺀다, 그래서 9가 된다.
2. 9는 3으로 나눠지니 3으로 나눈다.
3. 3은 3으로 나눠지니 3으로 나눈다
해서 연산을 총 3번 사용해서 10을 1로 만들어 냈으므로 출력값은 3입니다.
저것보다 더 적은 연산으로 10을 1로 만들어 낼 방법이 없습니다.
소스코드 & 설명
우선 본 문제는 매번 탐욕적인 선택(당장 보기에 최선의 선택)을 통해 최적해를 구하는 그리디 알고리즘을 사용하면 틀립니다. 문제를 처음 접근했을때는 수를 1로 빨리 만들어 내기 위해선 아래와 같이 현재 나눌 수 있는 수 중에 가장 큰 수로 나눠서 수를 팍팍 덜어내면 되겠구나 하는 생각이 듭니다.
1. 현재 나눌 수 있는 수 중에 최대한 큰 수로 나눈다
2. 1번이 안되면 1을 뺀다.
예를 들어서 10이 입력되면 일단 가장 큰 수인 3으론 나눌 수 없으니 2로 나누면 5, 5는 3이나 2로 나눠지지 않으니 어쩔 수 없이 -1 , 다시 4를 2로 나누고, 2를 2로 나누면 1이 나옵니다.
즉 10 -> 5 -> 4 -> 2 -> 1 로 연산이 4번 이루어졌습니다. 실제로 답은 4가 아닌 3으로써, 1을 가장 빨리 만들 수 있는 방법은 위에서 설명했듯이 10을 3이라는 큰 수로 나눠내기 위해 1로 먼저 빼서 9로 만들어주고 거기서 나누는 방식입니다.
그리디 알고리즘 자체는 미래를 봤을때 -1을 빼고 3을 나누는게 최적일지라도 뒷일은 생각하지 않고 일단은 당장 좋은 방법만 선택하기 때문에 해당 문제를 풀 수 없습니다.
즉 본 문제는 DP로 해결하는데 꼭대기인 10에서 목표값인 아래 1로 가는게 어려우니 TOP-Down 방식은 사용하지 않기로 하고 거꾸로 바닥부터 꼭대기까지 해결해 가는 Bottom-Up 방식을 사용해서 해결해야 합니다.
말이 좀 어려운데 10에서 1을 만드는게 아니라 1부터 차례대로 최소 연산의 수를 구해서 10까지 완성해내겠다는 뜻입니다. 아래 그림으로 설명하겠습니다.
우선 본 문제에서 입력 받는 정수 N의 경우 범위가 $1 <= N <= 10^6$ 입니다.
dp의 일반항을 구하기 전에 일단 입력에 따라 미리 알 수 있는 값을 생각해보겠습니다.
N == 1 : 연산을 시행할 필요가 없으므로 출력값은 0 입니다.
N == 2 : 1만 빼면 되므로 출력값은 1입니다.
N == 3 : 3으로 나누면 되므로 출력값은 1 입니다.
우선 N: 1~3 까지는 대충 생각이 됩니다. 문제 풀이를 위해 저걸 배열에 미리 입력하고 갈 것인데,
배열의 "인덱스"에 해당 하는게 N이고, 그 배열 인덱스의 "값"에 필요한 최소 연산의 수를 저장할 것입니다.
예를 들어서 arr이라는 배열이 있으면
1번 인덱스는 N == 1 으로 하고, 저장하는 값은 연산의 시행 횟수로 0입니다. (방금 위에서 구했던 것.)
arr[1] = 0 으로 저장합니다.
같은 방법으로 2번 인덱스는 N == 2 로 하고 출력값이 1이 였으므로 arr[2] = 1 로 저장합니다.
이런식으로 위에서 미리 구해 뒀던 3개의 값을 입력하고 시작합니다.
*N의 입력 범위가 1 이상이기 때문에 배열의 0번째 인덱스는 사용하지 않기로 하겠습니다.
arr[1] = 0, arr[2] = 1, arr[3] = 1 이 입력된 상태에서,
인덱스가 4, 즉 N == 4 일때 값을 어떻게 결정해야 하나 생각해보겠습니다.
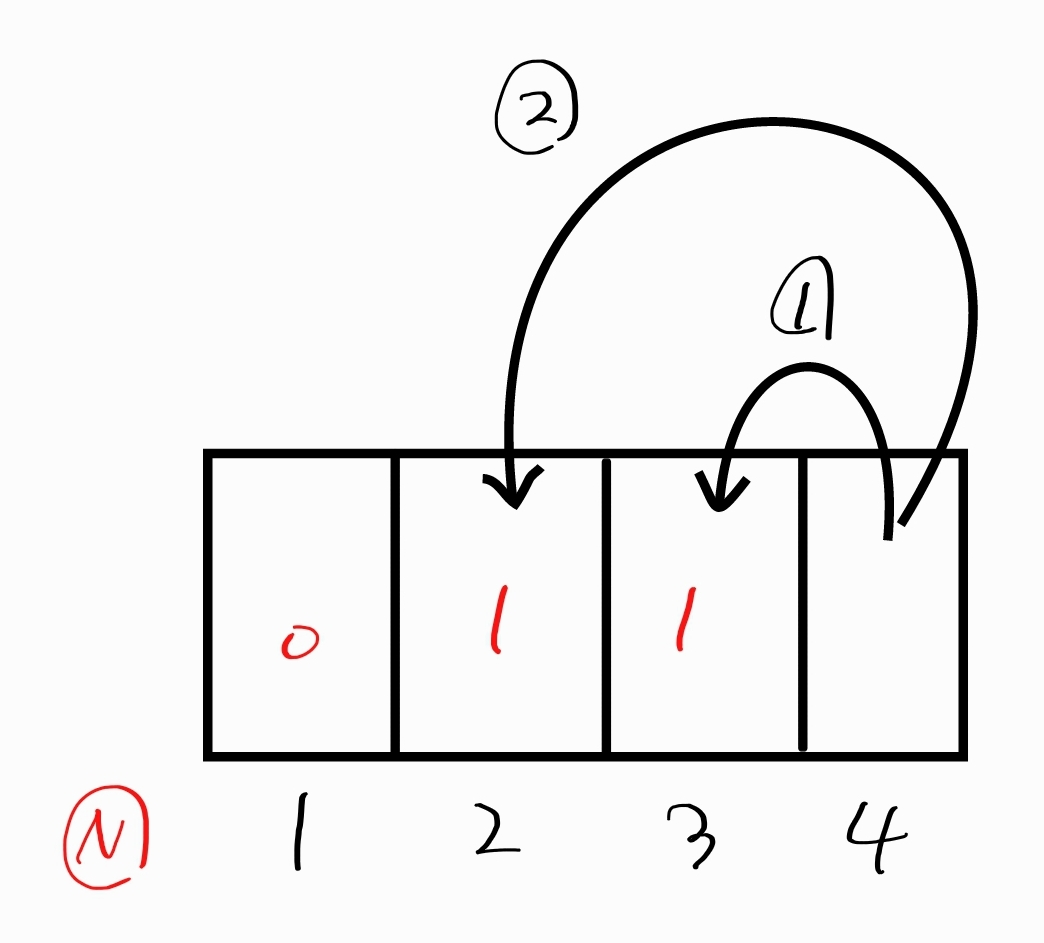
4라는 숫자의 입장에서 보면 최소 연산을 구하기 위해 두가지 선택을 할 수 있는데
우선 1번을 보면, 3이라는 숫자에서 1을 만드는 최소 연산의 값이 이미 1이라고 결정되어 있습니다. 그러면 4라는 숫자는 3이라는 숫자의 연산에서 1만 더해주면 완성이 되겠네요.
왜냐면 4에서 1을 빼면 3이 될 것이고, 그건 연산 횟수 1번이며 3이라는 숫자는 이미 최소 연산이 1번이라고 결정되어 있기 때문에 인덱스 4에는 2라는 값을 넣어주면 될 겁니다.
근데 이거만 있지 않습니다. 4라는 숫자는 2로 나눠지니깐 4를 2로 나눠서 4 -> 2가 되는 것도 고려 해야 합니다.
이럴땐 N=2 에서 연산이 몇 번 필요했는지 보고 1더하면 되겠죠. 위와 똑같습니다.
1과 2번 케이스 중에서 작은 값을 고르면 되겠군요. 이건 파이썬의 MIN() 함수 등을 이용하면 될겁니다.
즉, 반복문을 돌려서 i라는 숫자는 i-1 번째 인덱스에 해당하는 배열 값 + 1 , i가 3으로 나눠진다면 i // 3 번째 인덱스에 해당하는 배열값 + 1, i가 2로 나눠진다면 i // 2 번째 인덱스에 해당하는 배열값 + 1 을 해서
제일 적은 값을 선택해서 앞부터 차례대로 최소 연산의 수를 채워나가면 결론적으로 $O(N)$ 의 시간 복잡도로 문제를 해결 할 수 있는겁니다.
앞에서 최소 연산을 구한 걸 참고해서 값을 아래부터 완성시키는 방법입니다.
아래는 C++ 로 실제 구현한 소스코드입니다. 앞에선 배열을 예로 들었으나 편의를 위해서 STL Container인 Vector을 사용했습니다. 배열로 구현하고 싶으시면 N만큼 크기의 배열을 new로 동적할당해서 쓰시면 되겠습니다.
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int N;
cin >> N;
vector<int> v(N+1, 0); //N+1의 크기를 가지는 벡터를 생성, 모두 0으로 초기화
v = {0,0,1,1}; //0번째 인덱스는 편의를 위해 사용하지 않는다.
for (int i = 4; i <= N; i++){
v[i] = v[i-1] + 1;
if(i % 2 == 0 && v[i/2] + 1 < v[i]){
v[i] = v[i/2] + 1;
}
if(i % 3 == 0 && v[i/3] + 1 < v[i]){
v[i] = v[i/3] + 1;
}
}
cout << v[N];
return 0;
}
여기선 && 연산으로 조건을 비교해 가면서 i/2 , i/3 의 값들을 택했는데, 물론 min(v[i/3]+1, v[i])와 같은 방법으로 사용하셔도 됩니다. 왜 이렇게 작성했는진 아래 여담에 나옵니다.. ㅎㅎ
* C++에서 min() 함수는 std namespace에서 제공되는 것으로 파이썬에서 사용하는 것과 사용방법이 똑같습니다.
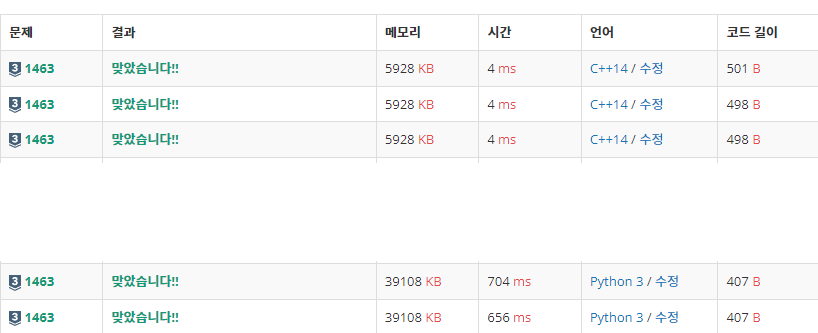
cin, cout의 sync를 풀어주지도 않았는데 C++로 제출하니 초광속으로 채점이 완료 되었네요.
역시 C++ 입니다. 시간은 4ms, 파이썬 풀이는 "704ms" 입니다...
여담
사실 이 문제는 푼지 상당히 오래됬는데 (아마 작년쯤에 풀었던걸로 기억합니다.) 갑자기 왜 뒷북을 치냐 하면 저번주 금요일 리눅스 시험 마지막 문제에 이 문제가 그대로 나와서 글을 쓰게 되었습니다 ㅎㅎ;;
쉘 스크립트랑 명령어 배우는 수업인데, 쉘 스크립트의 문법을 물어본것도 아니고 심지어 이 문제의 풀이 코드를 그대로 쉘 스크립트로 만들어 놓고 빈칸 채우기를 시키더라구요.
굉장히 당황스러웠습니다... 푼지 너무 오래되서 기억을 되살려서 반절정도 적었는데 if 문에 조건이 2개나 들어가 있어서 도대체 뭔가 했더만, 예전에 풀땐 파이썬의 min() 함수를 써서 if문 조건이 1개만 필요했는데 쉘 스크립트에는 그런 내장 함수가 제공되지 않으니 i - 1 번째에 들어간 값이 i // 2 의 값보다 작은지 if문으로 직접 비교하고 작으면 i // 2 + 1 의 값을 대입하는 방법이였더라구요 ㅜ ㅜ
시험이 끝나니 깨달음과 함께 이 문제의 해법을 작성하게 되었습니다.
(쉘 스크립트로 적고 싶었는데 그냥 귀찮아서 포기했습니다.)
마지막으로, 제가 문제 풀이에 도움을 받은 유투브 영상입니다.
https://www.youtube.com/watch?v=OSRD1bs9Om8
'프로그래밍 > BaekJoon' 카테고리의 다른 글
| [Baekjoon] 17626번: Four Squares (0) | 2022.05.01 |
|---|---|
| [Baekjoon] 5430번: AC (0) | 2021.07.20 |
| [Baekjoon] 10989번: 수 정렬하기 3 (0) | 2021.06.09 |
| [Baekjoon 파이썬] 1929번: 소수 구하기 (0) | 2021.06.03 |
| [Baekjoon C언어] 10250번: ACM 호텔 (5) | 2021.05.29 |









